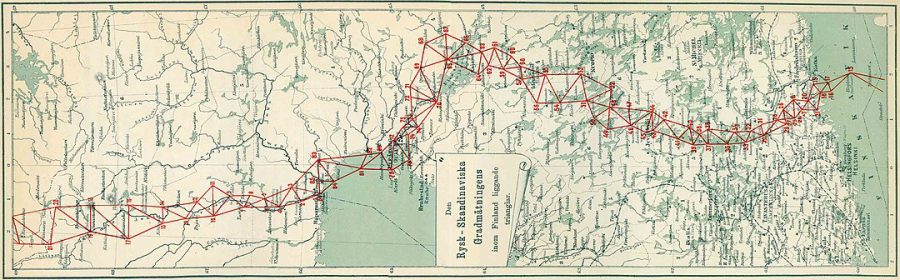
Kolmiolaskenta
Kuvaus: Tässä lukiolaisille suunnatussa tehtäväsarjassa tutkitaan kolmioita, sini- ja kosinilausetta, koordinaattijärjestelmää, gooneja sekä matematiikasta keskustelua.
Avainsanat: lukion matematiikka, geometria, kolmio, sinilause, kosinilause, gooni, maanmittaus, matematiikasta puhuminen
Johdanto
Matemaattinen keskustelu lukiossa
Kuuntele tai lue Lapin yliopiston matematiikan didaktiikan yliopistonlehtori Anna-Maija Partasen haastattelu matemaattisesta keskustelusta ja sen suhteesta lukio-opiskeluun.
Lue haastattelu
Asiantuntijana/haastateltava: Anna-Maija Partanen, Lapin yliopiston matematiikan didaktiikan yliopistolehtori ja LUMA-keskus Lapin johtaja
Haastattelija: Pekka Muotka, LaTu –hanke Rovaniemen kaupunki.
[Alkumusiikki]
Pekka Muotka
Millaista merkitystä matemaattisella keskustelulla voi olla lukio-opiskelijalle?
Anna-Maija Partanen
No ensinnä mä hahmotan tätä kahdella tavalla. Ensinnäkin matematiikasta keskusteleminen, sillä voi olla merkitystä oppimisen kannalta sekä yksilön oppimisen tai koko yhteisön yhteisön joko pienen ryhmän tai luokan oppimisen kannalta. Toinen on sitten, että tulevaisuuden ammateissa, missä sä matematiikkaa käytät, niin se ei ole enää nykyisin semmoista yksinäistä puurtamista, vaan kaikkialla tehdään tiimityötä ja sulla täytyy olla valmiuksia kommunikoida sun omia matemaattisia ajatuksia sen oman tiimisi kanssa, jotta sä voit olla semmoinen rakentava hedelmällinen työntekijä siinä tiimissä toimija siinä tiimissä.
Pekka Muotka
Minkälaista merkitystä nyt sillä matemaattisella keskustelulla voisi sitten olla sen matemaattisen oppimisen kannalta varsinkin yksilön näkökulmasta?
Anna-Maija Partanen
No okei tähän hän on oppimisteoriatkin, jotka puhuvat siitä jotain, mutta otetaanpa semmoinen esimerkki, että kun minä toimin lukion matematiikan opettajana ja oppilaalla oli jokin ongelma ja hän viittasi ja pyysi minulta apua, niin kun minä kävelin siihen oppilaan pulpetin viereen. Niin aika usein sattuu, että tämä opiskelija koksikin ‘’Ainiin – niinhän se onkin!’’. Eli mä ymmärrän sen niin, että kun hän valmistautui selittämään sitä ongelmaansa tai asiaa minulle, niinhän siinä jäsensi sitä omaa ajatteluaansa ja samalla huomasikin jotain uutta, jonka avulla hän pääsi siitä lähtemään eteenpäin. Eli kun me selitämme omaa tai edes valmistaudumme selittämään omaa ajatteluamme muille, niin meidän omat ajatukset jäsentyvät.
Mä muistan kun valmistelin väitöskirjaani ja oli semmoisia kinkkisiä ongelmia ja kerroin niistä. Oltiin miehen kanssa saunassa hyvin usein, kerroin saunakeskusteluissa hänelle niitä ajatuksia, niin eihän hän ymmärtänyt siitä minun väitöskirjan aiheesta niin juurikaan mitään, mutta minä sain paljon oivalluksia, koska kun minä kerroin niin minun omat ajatukset jäsentyvät ja tämä on monien monien kokemus.
Mutta sitten toisaalta myös yksilön kannalta, jos ajatellaan niin, jos sinä kuuntelet muita, kun he selittävät heidän omaa matemaattista ajatteluaan, niin jos se on erilaista kuin sinun, niin se aiheuttaa semmoisia ristiriitatilanteita. Meidän aivot on semmoisia, että ne kaipaavat semmoista tasapaino -tilannetta, että minä ymmärrän ja hallitsen tämän maailman, mutta jos sattuu semmoinen ristiriita, syntyy semmoinen ristiriitatilanne, niin meidän aivot on valmistautunut jotenkin järjestäytymään uudelleen selvittääkseen sen ristiriitatilanteen ja tämmöinen keskustelu voi antaa meille näitä ristiriitatilanteita, kokemuksia niistä ja jotka vaatii sitten meitä uudelleen organisoimaan ajatteluamme eli itseasiassa oppimaan.
[musiikkia]
Pekka Muotka
Mitä merkitystä matemaattisella keskustelulla on yhteisön oppimisen kannalta?
Anna-Maija Partanen
Nykyisin puhutaan paljon semmoisesta yhteisöllisestä tiedon kehittelystä ja mä oon kokenut sitä joissakin pienryhmissä ja myös semmoisissa isompien ryhmien keskusteluissa. Tässä on semmoinen käsite, joka on peräisin sosiaalisesta interaktiosta. Semmoinen kuin ‘’joint action’’, jota on oikeastaan niinku vähän vaikea suomentaa, mutta se tarkoittaa sitä, että kun ihmiset useampi ihminen on mukana keskustelussa vuoro vaikuttamassa, kuin kaikki esittävät omia ajatuksiaan ja kun sä kuuntelet muiden ajatuksia niin sä koko ajan suhteutat sitä omaa kommunikointia siihen mitä muut ovat sanoneet. Nyt tästä kaikesta syntyy semmoinen ryhmän tuottama keskustelu, joka on enemmän kuin osiensa summa. Se on enemmän kuin yksilöiden yksittäisten yksilöiden ajattelun summa. Ilman sitä sitä yhteisössä tapahtuvaa tiedon jakamista. Jos tällainen tilanne syntyy luokassa, mä oon joissakin tilanteissa nähnyt, että oppilaat keskustelevat ja opiskelijat keskustelevat hyvin intensiivisesti ja kommunikoida toistensa kanssa, niin siitä syntyy semmoinen oppimisympäristö, jossa jokainen voi jäsentää omaa ajatteluaan. Jokainen voi oppia, ne taitavimmat oppilaat, heikommat oppilaat, mutta myös opettaja voi oppia paljon oppilaiden ajattelusta ja erilaisista strategioista.
Pekka Muotka
Mitä merkitystä matemaattisella keskustelulla on työelämävalmiuksien kannalta?
Anna-Maija Partanen
No nyt jos ajatellaan nykyajan työelämää ja varsinkin tulevaisuuden työelämää, niin aivan varmasti tämmöinen tiimityöskentely ja osana verkostoja toimiminen lisääntyy. Niitä taitoja tarvitaan yhä enemmän ja enemmän ja silloin on tärkeätä osata ensinnäkin kommunikoida myös matematiikan parissa.
Niiden ihmisten työelämässä, jotka käyttävät matematiikkaa työssänsä. On tärkeätä osata kommunikoida omaa ajatteluaan ja toisaalta ymmärtää sitä mitä muut tarkoittavat ja jotta pystytään sen tiimin niin kuin työpanokset, niin kuin ohjaamaan samaan suuntaan ja todella toimimaan tiiminä.
Sitten semmoinen mitä mä oon viime aikoina erityisesti pohtinut on tämmöinen joustavuus siinä matemaattisessa ajattelussa, että myös opettajana toimivat tarvitsevat semmoista kykyä niin kuin ajatella, että joihinkin matemaattisiin tehtäviin on monia erilaisia ratkaisuja. Nimittäin, jos opettaja haluaa toimia tämmöisen nykyaikaisten oppimiskäsitysten mukaisesti, konstruktiivinen ja sosiokonstruktiivinen oppimiskäsitys, hänen täytyy pystyä kuuntelemaan, ottamaan selvää oppilaiden ajattelusta, jotta hän pystyy sen oman opetuksensa rakentamaan sen varaan tai sitten ohjailemaan tämmöistä keskustelua, josta juuri äsken oli puhetta. Niin opettajan tulee myös olla silleen ajattelulta joustava ja nähdä niinku niitä erilaisia matemaattisia strategioita, tai jotain matemaattisia menetelmiä, mutta myös matematiikkaa työksäkseen käyttävät, niin se joustavuus on, on minusta äärimmäisen tärkeätä, että jos vaikka jos sinulla on oma ratkaisu ja oma tie ja toisella on toisenlainen ratkaisu ja toisenlainen tie, mutta ne kumpikin ovat oikeita, niin jossakin vaiheessa joudutaan tekemään päätöksiä siitä, että nyt mennäänkin sen toisen tien mukaan, jolloin sun on niinku joustettava siinä omassa ajattelussasi ja nähtävä tämä toisen tien toisen ratkaisun mahdollisuudet.
Pekka Muotka
Mitä eroa on matemaattisella keskustelulla ja kirjallisella tuottamisella?
Anna-Maija Partanen
Tein oman väitöskirjatutkimukseni Rovaniemellä Lyseonpuiston lukiossa ja tutkin pienryhmien keskustelua. Tutkimme derivaatan käsitettä tutkivan oppimisen keinoin ja siellä minä niin kuin havahduin siihen, kun sitä oppilaiden keskustelua, pienryhmätyöskentely videoaineistoa analysoin niin, että suullinen ilmaisu oli ihan, ja puhe matematiikasta, oli ihan erilaista kuin sitten kun tutkimuksen lopuksi opiskelijoiden tuli kirjoittaa siitä tutkimuksesta yhteenveto eli keskustelussa voidaan tehdä semmoisia ehdottavia, ajatuksia ehdottavia näkökulmia ja esittää luovia erilaisia näkökulmia ja ehkä löytää sitä löytää uusia merkityksiä niille asioille. Mutta sitten kun nämä opiskelijat ryhtyivät kirjoittamaan sitä yhteenvetoa, niin huomasin, että he käyttivät täsmällistä kieltä, käyttivät oikeita nimityksiä niille termeille, ilmaisivat asioita tiiviisti ja symbolisesti. Niin jotenkin se kirjoitettu kieli sitten vielä niin kuin kirjoitetun kielen avulla ilmastu yhteenveto jotenkin niin kuin tiivisti sen mitä keskustelussa luovassa keskustelussa oli löydetty, niin tiiviisti sen sitten niinku matematiikan kielellä.
[Loppumusiikki]
Maanmittauksen opiskelua, työskentelyä alalla ja matematiikkaa
Kuuntele tai lue ammattikorkeakoulun maanmittaustekniikan koulutuksessa opiskelevan ja alalla työskentelevän Maiju Mäkitiuran ajatuksia maanmittauksesta, sen opiskelusta ja alalla työskentelystä. Näkökulmia alasta ja sen suhteesta matematiikkaan.
Lue haastattelu
Asiantuntijana/haastateltava: Maiju Mäkitiura, Lapin ammattikorkeakoulun opiskelija
Haastattelija: Pekka Muotka, LaTu –hanke Rovaniemen kaupunki.
Pekka:
Kertoisitko itsestäsi?
Maiju:
Olen Maiju Mäkitiura ja opiskelen Lapin ammattikorkeakoulussa maanmittausinsinööriksi ja tällä hetkellä opintoni on loppuvaiheessa ja opintojen ohessa työskentelee infra puolella mittausharjoittelijana.
Pekka:
Miten päädyit opiskelemaan maanmittausinsinööri?
Maiju:
No lukiossa oli hyvin epävarmaan, että mitä lähden opiskelemaan ja abivuonna olin hyvin kiinnostunut matematiikasta ja maantieteestä ja päädyin sitten lukemaan jotakin ammattikorkeakoulun esitettä ja tää maanmittaustekniikan opinnot kuulosti semmoselta hyvältä yhdistelmältä matematiikan ja maantieteen välillä ja päädyinkin pääsemään opiskelemaan ja tässä sitä ollaan.
Pekka:
Millaista se opiskelu maanmittausinsinöörin koulutuksessa oikein on?
Maiju:
No lukio-opintoihin verrattuna on paljon enemmän itsenäisyyttä ja vapautta ja vapauden mukana tulee aina vastuuta niistä omista opinnoista ja niiden etenemisestä ja meidän oppinahjossa, jossa korostuu hyvin pitkälti ryhmätyöskentely ja meillä on tämmöisiä erilaisia lukukausiprojekteja, joissa sitten nää tehdään ryhmissä erilaisia tehtäviä ja näihin projekteihin yhdistetään aina sitten nämä muut lukukauden opintojaksot.
Pekka:
Se kuulostaa tosi mielenkiintoiselta juttua, että siellä pääsee sitten ryhmätyöskentelemään ja se on semmoista sosiaalista oppimista kanssa siinä samassa.
No entä miten siellä opinnoissa sitten näkyy se matematiikka osana muita opintoja?
Maiju:
Matematiikkaa opiskellaan pääasiassa edellisillä matematiikan opintojaksoilla, mutta sitten muutoin se näkyy aika lailla semmoisena soveltamisena kaiken taustalla ja monella opintojaksolla sitten tehdään esimerkiksi lasketaan jollain kaavoilla jotakin, niin toki niissä näkyy taustalla myös se matematiikka, mutta sitten oman mielenkiinnon mukaan pystyy myös lukemaan vähän pidemmälle matematiikkaa.
Pekka:
Millaiseksi koet siirtymään sieltä ammattikorkeakoulun opinnoista työelämään?
Maiju:
No tekniikan alalla on yleensä muulloinkin tämä tilanne, että koulun penkiltä aikalailla revitään sinne työelämään ja töissä pääsee hyvin erilaisiin tai erityyppisiin tehtäviin ja maanmittausalan on ylipäänsä hyvin laaja-alainen. Se maanmittausinsinöörin työ voi olla asiakaspalvelua, toimistotyötä tai maastotyötä ja usein se on näiden kaikkien yhdistelmää. Omassa työssäni minulla on pääasiassa puoliksi siten, että on toimistotyötä ja sitten maastotyöstä. Töitä on tosiaan tarjolla hyvin monipuolisesti erilaisissa tehtävissä.
Pekka:
Joo se kuulostaa kyllä tosi monipuoliselta tuo mitä kaikkea pääsee oikein tekemään.
No entä miten se matematiikka näkyy siellä työssä?
Maiju:
Semmoista perinteistä laskemista on hyvin vähän, että pääasiassa koneet laskevat meillä kaiken tarvittavan, mutta kuten ylipäänsäkin aina insinöörin työssä, niin semmoinen yleisymmärrys siitä matematiikasta on. Niinku oltava ja se matematiikka näkyy koko ajan siellä taustalla, että varsinkin silloin korostuu, kun tulee joku ongelma, jossa esimerkiksi jossain mittauksessa niin, jotta osataan sitten alkaa ratkomaan sitä ongelmaa oikeasta paikasta niin pitää ymmärtää ne ilmiöt siellä mitä se kone laskee.
Pekka:
Kiitos Maiju sinulle haastattelusta.
Maiju:
Kiitos.
Tehtävä 1:
Suunnistusta ETRS-TM35FIN –koordinaatistossa kolmioiden ominaisuuksia hyödyntäen.
Ohje
Lähtöpiste
Harjoittele ja ratkaise:
- Kun patsaalta kuljetaan 2610,1 m suuntaan 197,48° voi löytyä mielenkiintoinen opiskelupaikka. Mikä?
- Kun patsaalta kuljetaan 837,6 m suuntaan 321,03° voi löytyä kaunis näkymä. Missä olet?
- Selvitettyäsi paikat voit käydä katsomassa näkymän palvelusta Google Maps.
Haasta kaverisi
4. Kehitä samalla idealla suunnistustehtävä kaverillesi.
Tehtävä 2:
Mittaus- ja kartoitustekniikan perusteita
Ohje
Katso video, määritä käsitteitä sekä laske pisteiden koordinaatteja.
Katso video
Principles of Surveying // Fundamental Principles of Surveying // Surveying Basics (3:07)
Selvitä:
- Pisteen koordinaattien määrittäminen kahden verrokkipisteen avulla.
- Kokonaisuudesta osiin etenemisen periaate.
Laskutehtäviä:
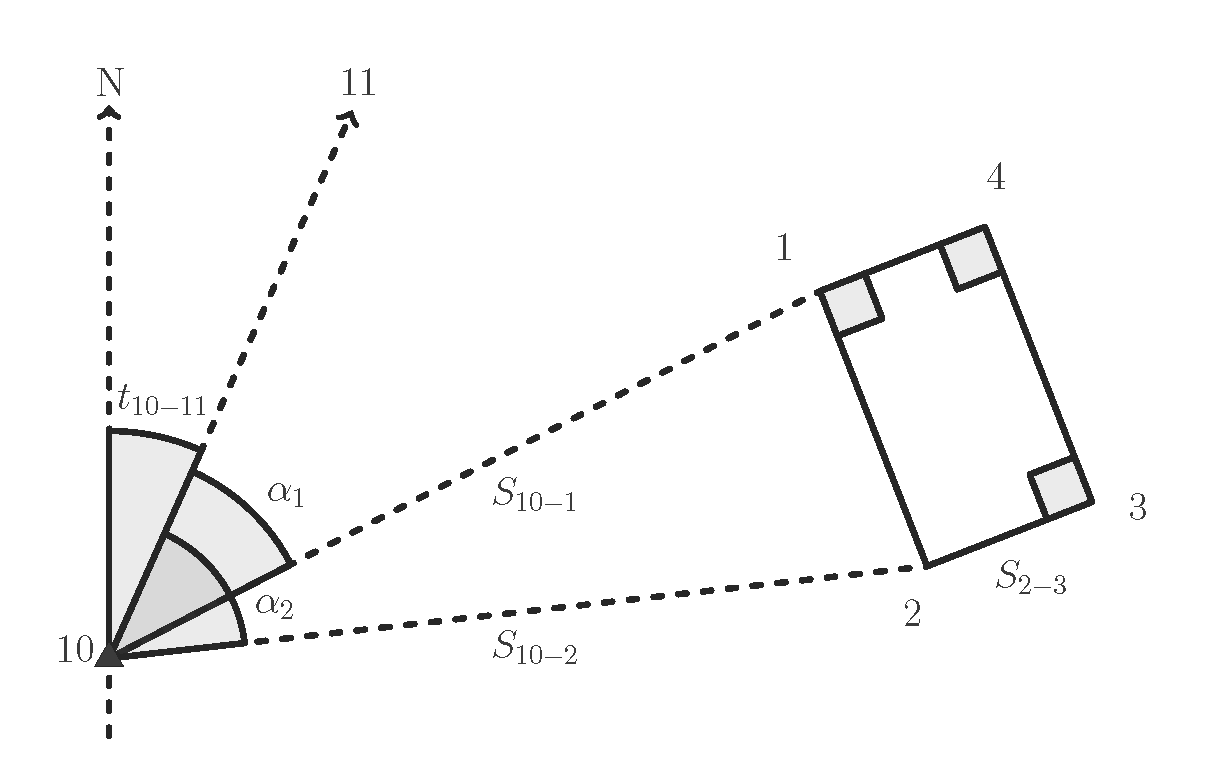
Kuvan esittämän suorakulmaisen rakennuksen nurkat 1 ja 2 mitattiin säteittäisellä mittauksella asemapisteeltä 10. Kojeelle näkymättömien nurkkien määrittämiseksi mitattiin mittanauhalla sivu 2 – 3. Olkoon X10 = 1158.183 m ja Y10 = 2392.165 m, t10-11 = 26.6088 gon, α1 = 43.034 gon, s10-1 = 67.739 m, α2 = 66.254 gon, s10-2 = 69.696 m ja s2-3 = 15.00 m.
A) Rakennuksen nurkkien 1 ja 2 koordinaatit
B) Rakennuksen nurkkien 3 ja 4 koordinaatit
Tehtävä on muunnelma Pasi Laurilan kirjan tehtävästä. Katso lisää vastaavia maanmittausalan tehtäviä Lapin ammattikorkeakoulun sivuilta.
Tehtävä 3:
Kolmioverkko
Ohje
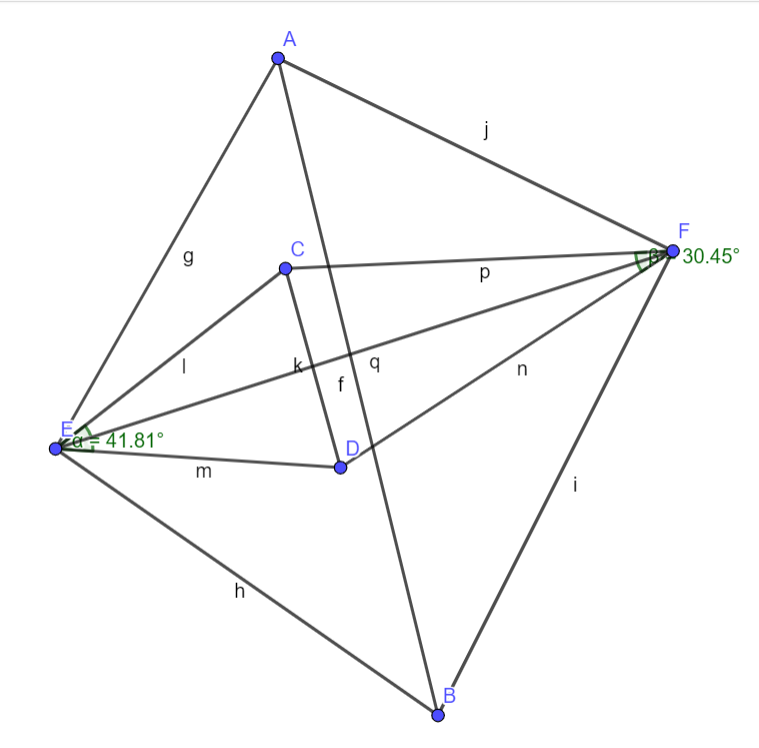
Katso video, laske kolmioverkon pääviivan pituus ja keskustele sini- ja kosinilauseesta.
Katso video
Kolmiomittaus – Suomen kartoituksen perusta (32:35)
Tehtävän 3 laskemiseen katso tarkasti videolta kohta (10:33-12:15).
Laske:
Keskustele parin kanssa:
Milloin voidaan käyttää sinilausetta ja milloin kosinilausetta kolmion osien ratkaisemisessa?
Tehtävä 4:
Kaukoputkea kääntämässä?
Ohje
Laske kuinka paljon kaukoputkea on käännettävä.
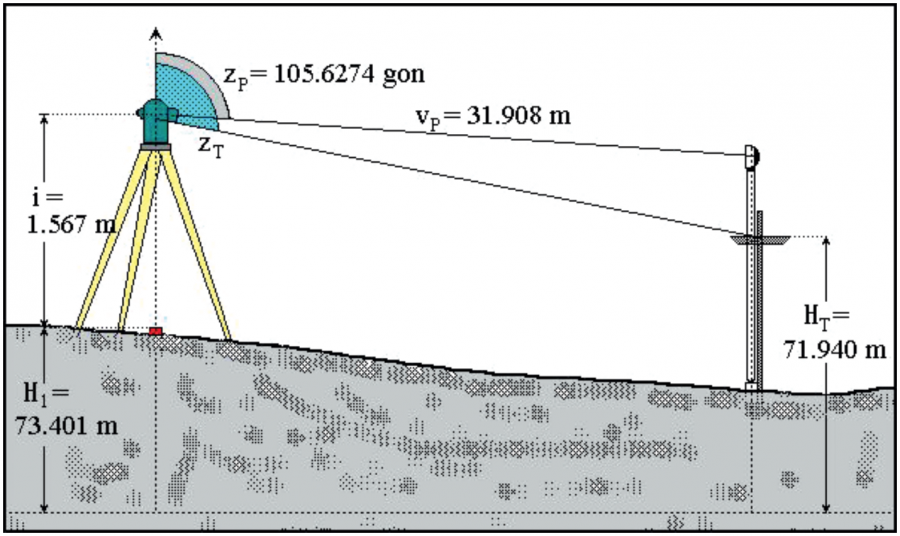
KUVA: Korkeuden merkintä takymetrillä. CC BY-NC-SA 3.0, Pasi Laurila
Laske:
Korkeuden tähtäysmerkki asetettiin paikalleen takymetrillä kuvan esittämällä tavalla. Asemapisteen korkeus oli H1 = 73.401 m ja kojekorkeus oli i = 1.567 m. Takymetrillä havaittiin mittalinjan paalulla olevaan prismaan pystykulma zP = 105.6274 gon ja vinoetäisyys vP = 31.908 m.
Kuinka paljon kaukoputkea oli käännettävä pystytasossa, jotta tähtäys osui kiinnitysrimaan tavoitekorkeuden HT = 71.940 m kohdalle? (KUVA: Korkeuden merkintä takymetrillä.)
Tehtävä on teoksesta ”Mittaus- ja kartoitustekniikan perusteet”, 2012. Julkaistu tekijänluvalla LaTu -hankkeen materiaaleissa 2021.
Keskustele parin kanssa:
Milloin voidaan käyttää sinilausetta ja milloin kosinilausetta kolmion osien ratkaisemisessa? (KUVA: Korkeuden merkintä takymetrillä.)
Yhteistyössä
Teuvo Heimonen, Lapin ammattikorkeakoulu, AMK-tutkinnot insinööri (AMK), Maanmittaustekniikka
Maiju Mäkitiura
Anna-Maija Partanen, Lapin yliopisto sekä LUMA-keskus Lappi
Janne Oinas, Lyseonpuiston lukio
Pasi Laurila
Kolmiomittaus – Suomen kartoituksen perusta -video